
1. 문제 정의 및 예제 해석
(문제 링크: https://www.acmicpc.net/problem/2156)
2156번: 포도주 시식
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규
www.acmicpc.net

처음에 포도주 개수(n)가 주어지고, 다음에 n 줄에 걸쳐 각 포도주 잔에 들어있는 포도주의 양이 주어진다.
6 : 포도주 개수(n)
6 : 첫 번째 포도주 잔의 포도주 양
...
1 : 마지막 포도주 잔의 포도주 양
입력받은 포도주 잔의 포도주양을 리스트로 만들면 [6, 10, 13, 9, 8, 1]와 같습니다. 이제 연속으로 3잔 선택하지 말라는 규칙을 만족하면서, 최대의 포도주 양을 만들어 출력합니다.
2. 전체 코드
## 일반 풀이
n=int(input())
p=[int(input()) for _ in range(n)]
dp=[0]*(n+1)
dp[1]=p[0]
if n>=2:
dp[2]=p[0]+p[1]
for i in range(3,n+1):
dp[i]=max(dp[i-3]+sum(p[i-2:i]), dp[i-2]+p[i-1], dp[i-1])
print(dp[n])
## 숏코딩 풀이
a=[int(input())for i in range(int(input()))]
d=[0,a[0]]
for i in a[1:]:
d=[max(d),d[0]+i,d[1]+i]
print(max(d))
3. 일반 풀이 해설
1) 입력 및 dp table 생성
n=int(input())
p=[int(input()) for _ in range(n)]
dp=[0]*(n+1)
dp[1]=p[0]* 코드 설명
n은 포도주 개수이고, p는 n번 반복하며 각 포도주 잔의 포도주 양을 입력받습니다. dp 리스트는 k번째 인덱스에서, 위 규칙을 만족하며 포도주잔 순차적으로 k개를 선택했을 때 최대의 포도주양을 저장할 리스트입니다. dp[1]은 첫 번째 포도주 잔만 선택하여 만든, 최대의 포도주 양이므로, p[0]인 첫 번째 포도주 잔의 포도주양을 저장합니다.
*출력
위 예제에 대해 위 코드 실행결과, p와 dp를 출력해보겠습니다.
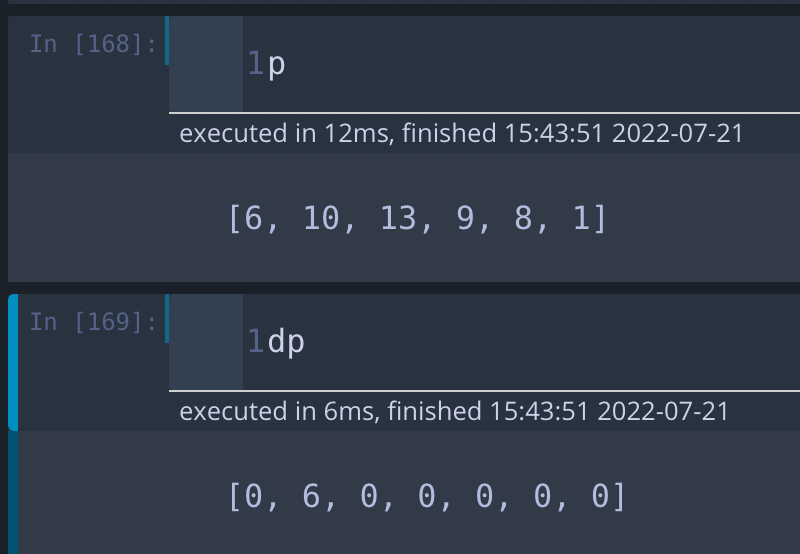
2) 핵심 알고리즘
if n>=2:
dp[2]=p[0]+p[1]
for i in range(3,n+1):
dp[i]=max(dp[i-3]+sum(p[i-2:i]), dp[i-2]+p[i-1], dp[i-1])
print(dp[n])* 코드 설명
n이 2 이상일 때, dp[2]=p[0]+p[1]입니다. dp[2]는 첫 번째와 두 번째 포도주잔의 포도주양으로 규칙(연속 3개 포도주잔 선택 못함)을 만족하며 만들 수 있는 최대의 포도주 양으로, 첫 번째와 두 번째 잔의 양을 합친 값이기 때문입니다. n이 1일 때는 p[1]인 두 번째 잔이 없기 때문에 에러가 발생해 if문으로 n이 2 이상일 때만 보았습니다. 다음으로, 3부터 n까지 for문을 돌며, dp[i]=max(dp[i-3]+sum(p[i-2:i]), dp[i-2]+p[i-1], dp[i-1])를 반복합니다. 예제와 함께 과정을 살펴보겠습니다. (여기서 헷갈릴 수 있는 부분이 dp는 1-based 인덱스이고, p(포도주 리스트)는 0-based 인덱스입니다.)
<포도주잔에 따른 포도주양 리스트>
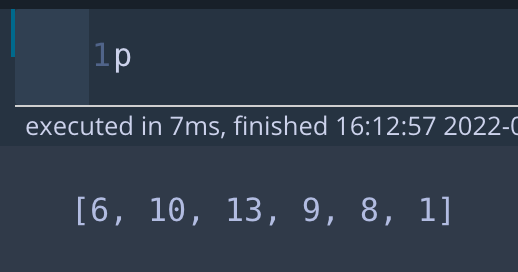
* i=3 일 때, dp[3] - 세 번째 포도주까지로 만들 수 있는 최대의 포도주 양 => 아래 3개 중 가장 큰 23
- dp[i-3]+sum(p[i-2:i]) : 0번째까지 포도주 최대의 양(0)에 2번째, 3번째 포도주의 양을 더한 값. 즉, 10 + 13 = 23
- dp[i-2]+p[i-1] : 1번째 까지 포도주 최대의 양(6)에 3번째 포도주의 양을 더한 값. 즉, 6 + 13 = 19
- dp[i-1] : 2번째까지 포도주 최대의 양. 즉, 16
- 여기까지 dp 출력

* i=4 일 때, dp[4] - 네 번째 포도주까지로 만들 수 있는 최대의 포도주 양 => 28
- dp[i-3]+sum(p[i-2:i]) : 1번째까지 포도주 최대의 양(6)에 3번째, 4번째 포도주의 양을 더한 값. 즉, 6+13+9=28
- dp[i-2]+p[i-1] : 2번째까지 포도주 최대의 양(16)에 4번째 포도주의 양을 더한 값. 즉, 16 + 9 = 25
- dp[i-1] : 3번째까지 포도주 최대의 양. 즉, 23
- 여기까지 dp 출력
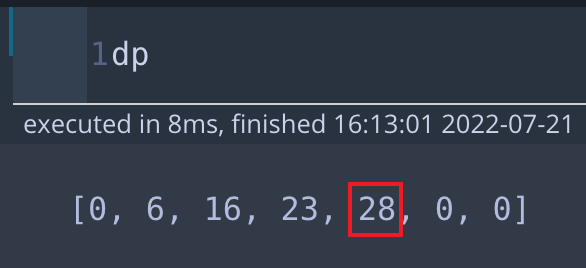
이렇게 dp에서 k번째까지 최대 포도주의 양을 갱신해가며 for문을 도는 게 핵심 알고리즘입니다. 아마 DP가 익숙지 않으시면, 이 부분이 이해하기가 정말 어려울 것입니다. 저도 쓰면서 어떻게 하면 더 쉽게 설명할 수 있을까 고민했는데, 정말 쉽지 않습니다. 핵심은 dp 리스트에서 k번째가 처음부터 k개의 포도주로 만들 수 있는 최대의 양이라고 가정하고, k+1번째에 어떤 값들을 비교해서 max값을 해야 k+1번째에 포도주가 최대의 양이될지를 고민하는 것입니다.
4. 숏 코딩 해설
숏 코딩 풀이 중에 정말 짧고 pythonic 하지만, 이해하기 어려운 풀이를 발견하여 설명드려봅니다.
a=[int(input())for i in range(int(input()))]
d=[0,a[0]]
for i in a[1:]:
d=[max(d),d[0]+i,d[1]+i]
print(max(d))* 코드 설명
a에는 리스트 컴프리헨션을 통해 바로 포도주의 양 리스트를 받습니다. 위의 p 리스트와 똑같은 리스트입니다. dp 리스트를 d라는 변수에 저장합니다. d=[0,a[0]]로 초기화하는 이유는, 1-based이기 때문에 0번째를 0으로 지정하고, 포도주가 1개 이상 주어지기 때문에 1 인덱스에 a[0]을 저장합니다. 여기서 1-based란 건 첫 번째 인덱스가 첫 번째 포도주까지의 최대 양으로 인덱스와 포두저 번째를 맞추기 위함입니다. 즉, 첫 번째 값의 인덱스를 1번 인덱스로 맞춰주는 것입니다. 다음으로 두 번째 포도주부터 for문으로 반복하며 d= max(d),d[0]+i,d[1]+i]를 수행해줍니다. 이 부분이 이해하기 굉장히 어려운 부분입니다. 예제에 대해 순차적으로 보겠습니다.
<포도주양 리스트인 a 출력>
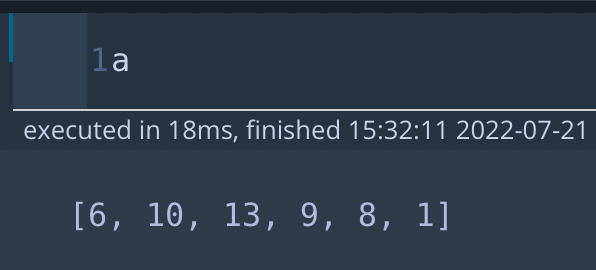
* 첫 번째로 i=10 일 때, 2번째 포도주부터 시작
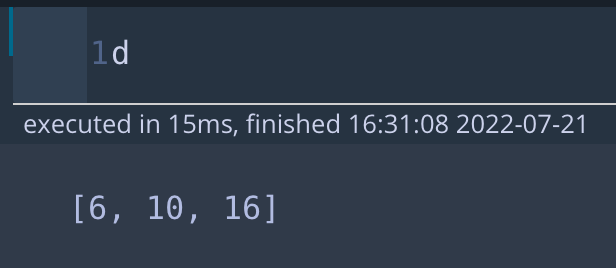
- max(d) : 1번째 포도주까지 포도주 최대의 양(6) → 6
- d[0] + i : 0번째 포도주까지 최대 양(0) + 2번째 포도주(10) → 10
- d[1] + i : 1번째 포도주까지 최대양(6) + 2번째 포도주(10) → 16
- 여기까지 d 출력
* 두 번째로 i=13 일 때, 3번째 포도주부터 시작
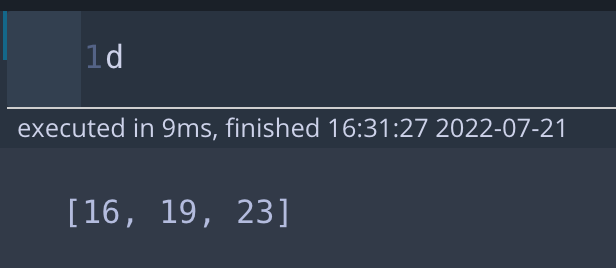
- max(d) : 2번째 포도주까지 포도주 최대의 양(16) → 16
- d[0] + i : 1번째 포도주까지 최대 양(6) + 3번째 포도주(13) → 19
- d[1] + i : 0번째 포도주까지 최대양(0) + 2번째 포도주(10) + 3번째 포도주(13) → 23
-> 이 부분이 이해 하기가 정말 어렵습니다. 이 부분은 2번째까지 포도주의 최대 양이 아니라, 0번째까지 포도주 최대의 양 + 2번째 + 3번째 포도주의 양이 됩니다.
- 여기까지 d 출력
* 세 번째로 i=9 일 때, 4번째 포도주부터 시작
- max(d) : 3번째 포도주까지 포도주 최대의 양(23) → 23
- d[0] + i : 2번째 포도주까지 최대 양(16) + 4번째 포도주(9) → 25
- d[1] + i : 1번째 포도주까지 최대양(6) + 3번째 포도주(13) + 4번째 포도주(9) → 28
-> 이 부분을 한 번 더 보면 패턴이 보입니다. 위에 i=13일 때 d[0]+i를 보면 1번째 포도주까지 최대 양(6) + 3번째 포도주(13)가 이 부분의 d[1]을 의미하고 여기에 i(4번째 포도주의 양)을 더해준 것입니다. 다음 반복에서는 위의 d[0]+i를 이용해 2번째 + 4번째 + 5번째 가 되겠습니다.
- 여기까지 d 출력

5. 느낀 점
숏 코딩 풀이를 이해하는 게 정말 어려웠습니다. 저 풀이는 DP 문제에 대해 점화식을 세우는 게 완전히 익숙해졌을 때, 메모리 사용량까지 줄여버리는 DP 리스트를 생성하는 풀이입니다. dp리스트가 계속 3개짜리가 갱신되면서도, 최댓값을 계속 추적합니다. 특히 d [1]+i 부분이 어려웠습니다. 이 부분은 현재 단계에서 전 전 전 단계의 최댓값 + 전 포도주양 + 현재 포도주양으로 계산될 뿐만 아니라, 처음에는 첫 번째까지 포도주 최대양 + 2번째 포도주양으로 초기화까지 해줍니다. 이 풀이를 이해하는데만 몇 시간이 걸렸는지 모르겠습니다. 아직 제대로 이해한 게 맞는지도 모르겠습니다. DP 알고리즘은 뭔가 지금 생각하는 것에서 한 발자국 뒤로, 또 한 발자국 뒤로 가며 메타인지를 계속 상승시키는 기분이 듭니다. 정말 사람이 할 짓이 아닌 것 같습니다.
읽어주셔서 정말 감사합니다.
다음에 더욱 재미있고 유익한 글로 찾아오겠습니다.
'Programming > 알고리즘' 카테고리의 다른 글
| [백준] 2579 계단 오르기 (DP) - Python / 자세한 설명 / 실버3 (0) | 2022.07.24 |
|---|---|
| [Python] 정수 및 배열 입력 받기 (알고리즘 입력) / sys.stdin.readline(입력 빠르게하기) (0) | 2022.07.23 |
| [백준] 2294 동전 2 - Python (DP) (0) | 2022.07.19 |
| [백준] 2606 바이러스 - Python (그래프 탐색) (8) | 2022.07.17 |
| [백준] 14248 점프 점프 - Python (그래프 탐색) (0) | 2022.07.16 |