
1. 문제 정의 및 예제 해석
(문제 링크: https://www.acmicpc.net/problem/2579)
2579번: 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
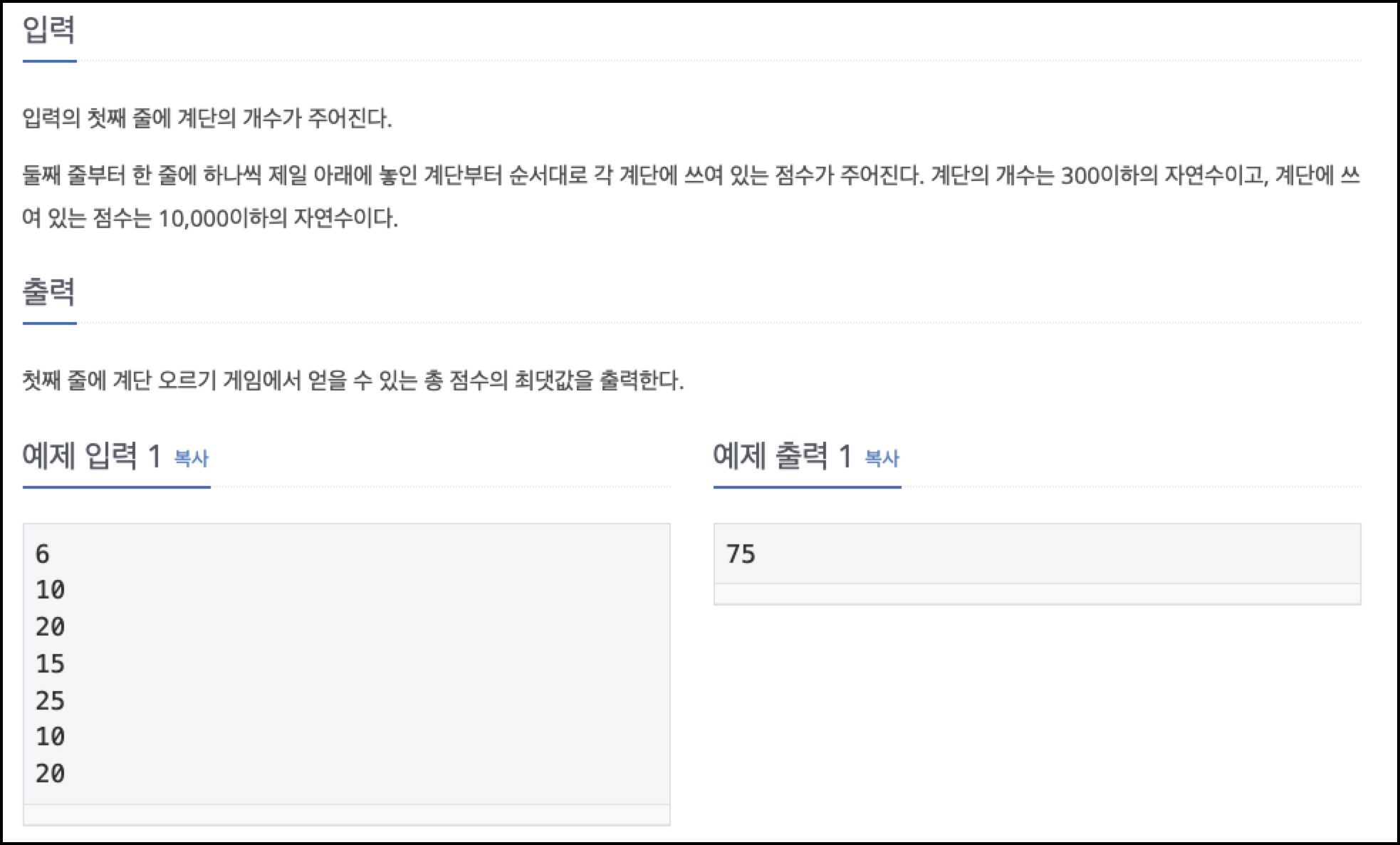
6 : 아래 주어질 계단의 개수
10 : 첫 번째 계단의 점수
20 : 두 번째 계단의 점수
..
20 : 마지막(6번째) 계단의 점수
이제 아래 3가지 규칙에 따라 계단을 오를 때, 최대 점수를 출력해야 합니다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
2. 전체 코드
n=int(input()) # 계단 개수
s=[int(input()) for _ in range(n)] # 계단 리스트
dp=[0]*(n) # dp 리스트
if len(s)<=2: # 계단이 2개 이하일땐 그냥 다 더해서 출력
print(sum(s))
else: # 계단이 3개 이상일 때
dp[0]=s[0] # 첫째 계단 수동 계산
dp[1]=s[0]+s[1] # 둘째 계단까지 수동 계산
for i in range(2,n): # 3번째 계단 부터 dp 점화식 이용해서 최대값 구하기
dp[i]=max(dp[i-3]+s[i-1]+s[i], dp[i-2]+s[i])
print(dp[-1])
3. 일반 풀이 해설
1) 입력 및 dp 정의
n=int(input()) # 계단 개수
s=[int(input()) for _ in range(n)] # 계단 리스트
dp=[0]*(n) # dp 리스트* 코드 설명
n에 계단개수를 입력받고, s에는 각 계단의 점수를 리스트로 입력받습니다. dp는 n개의 0으로 채워진 리스트를 생성합니다.
2) 계단이 2개 이하일 때
if len(s)<=2: # 계단이 2개 이하일땐 그냥 다 더해서 출력
print(sum(s))* 코드 설명
계단이 2개 이하라면, 1개일 땐 그 계단 점수가 최대이고, 2개일 땐 2개 계단의 점수를 합한 게 최대입니다. 그러므로, s(계단 점수 리스트)를 sum 하여 출력합니다.
3) 계단이 3개 이상일 때
else: # 계단이 3개 이상일 때
dp[0]=s[0] # 첫째 계단 수동 계산
dp[1]=s[0]+s[1] # 둘째 계단까지 수동 계산
for i in range(2,n): # 3번째 계단 부터 dp 점화식 이용해서 최대값 구하기
dp[i]=max(dp[i-3]+s[i-1]+s[i], dp[i-2]+s[i])
print(dp[-1])* 코드 설명
dp리스트는 각 인덱스에 최대 점수가 들어갑니다. 예를 들어, dp[0]에는 첫 번째 계단까지의 최대 점수가 들어가고, dp[1]에는 두 번째 계단까지의 최대 점수가 들어갑니다. dp[0]과 dp[1]은 각각 첫 번째 계단과 두 번째 계단까지 점수의 합으로 초기화해줍니다. 그리고 인덱스 2(3번째 계단)부터 n까지 for문을 통해 반복하며 dp를 갱신해줍니다. 핵심 코드는 dp[i]=max(dp[i-3]+s[i-1]+s[i], dp[i-2]+s[i]) 입니다.
쪼개서 살펴보겠습니다. 아래 2개 중 max값을 dp[i]에 할당해줍니다.
- dp[i-3]+s[i-1]+s[i] : i-3까지의 계단 점수 최댓값과 i-1, i 계단의 합.
- dp[i-2]+s[i] : i-2까지의 계단 점수 최댓값과 i 계단의 합.
이 의미는, 3번째 계단부터 2계단을 연속으로 걸었을 때와, 1계단을 건너뛴 것을 비교해서 최댓값을 계속 갱신시켜나가는 것입니다. 이 부분이 굉장히 어려운데, i를 3부터 넣어서 차근차근 하나씩 대입해보면, dp[i]가 i 계단까지 점수의 최댓값을 항상 보장한다는 것을 알 수 있습니다.
4. 느낀 점
전형적인 dp 문제입니다. 3가지 규칙을 어떻게 점화식으로 바꾸는지가 관건이었습니다. 저는 특히, 연속으로 3개를 걸을 수는 없지만, 꼭 1개나 2개를 걸어야 하며, 마지막 계단은 꼭 밟아야 하는걸 동시에 만족시키는 점화식이 도저히 떠오르지 않아, 복잡한 코드로 풀다가 포기하고, 차근차근 다시 접근하여 풀었습니다. dp 문제는 첫 번째, 두 번째가 채워진 dp 리스트에 대해 세 번째를 어떻게 만족시킬 것인지, 그게 네 번째까지 보장을 해주는지에 집중하면 그나마 좀 쉽게 풀리는 것 같습니다.
읽어주셔서 정말 감사합니다.
다음에 더욱 재미있고 유익한 글로 찾아오겠습니다.
'Programming > 알고리즘' 카테고리의 다른 글
| [백준] 1912 연속합 (DP) - Python / 자세한 설명 / 실버2 (0) | 2022.07.26 |
|---|---|
| [백준] 1463 1로 만들기 (DP) - Python / 자세한 설명 / 여러가지 풀이 / 실버1 (6) | 2022.07.25 |
| [Python] 정수 및 배열 입력 받기 (알고리즘 입력) / sys.stdin.readline(입력 빠르게하기) (0) | 2022.07.23 |
| [백준] 2156 포도주 시식 - Python 자세한 설명 (DP, 숏코딩) (0) | 2022.07.21 |
| [백준] 2294 동전 2 - Python (DP) (0) | 2022.07.19 |