
이번엔 백준 12015 가잔 긴 증가하는 부분 수열 2 문제를 Python을 이용해 풀어보겠습니다. 12738 가장 긴 증가하는 부분 수열3 역시 아래와 풀이가 완전 동일합니다.
* 12015 문제 링크
12015번: 가장 긴 증가하는 부분 수열 2
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000,000)
www.acmicpc.net
* 12738 문제 링크
12738번: 가장 긴 증가하는 부분 수열 3
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (-1,000,000,000 ≤ Ai ≤ 1,000,000,000)
www.acmicpc.net
*전체 코드
from bisect import bisect_left
N=int(input())
A=list(map(int,input().split()))
dp=[]
for num in A:
k = bisect_left(dp,num)
if len(dp) == k:
dp+=[num]
else:
dp[k]=num
print(len(dp))
문제 정의
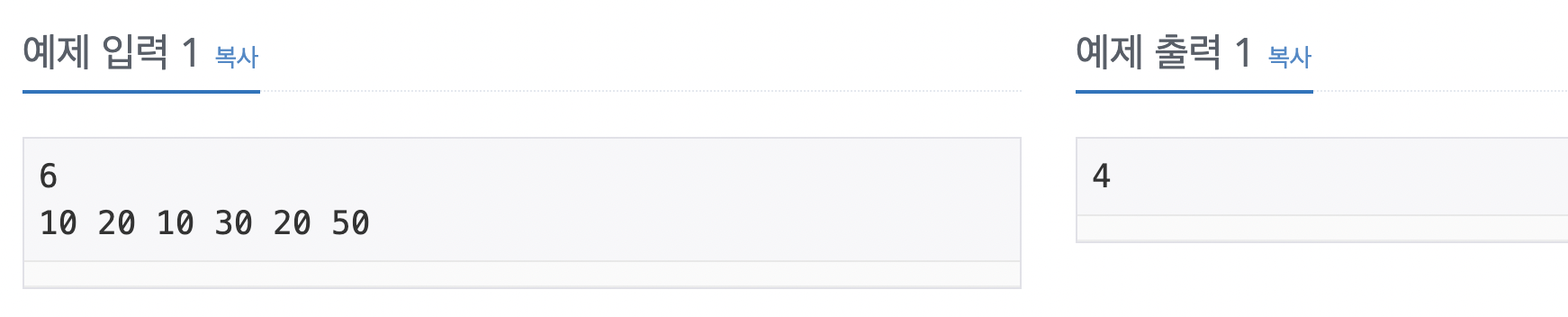
첫째 줄에는 1이상 100만 이하의 정수가 주어지고, 둘째 줄에는 그 개수만큼의 수열(수의 나열)이 주어집니다. 수열 역시 1~100만 정수로 이루어져 있고, 출력은 가장 긴 증가하는 부분 수열의 길이입니다. 여기서 부분수열은, 띄엄띄엄 도 가능합니다. 아래 예제에서 A = {10, 20, 10, 30, 20, 50} 이고, 가장 긴 증가하는 부분 수열의 길이는 4이다.
(12738 가장 긴 증가하는 부분 수열3 에서는 각 수열의 숫자 범위가 -1억 ~ 1억인 점만 다르기 때문에, 아래 풀이와 완전 동일합니다.)
1. bisect_left 임포트 및 입력부
from bisect import bisect_left
N=int(input())
A=list(map(int,input().split()))
dp=[]1) bisect 간단 설명
bisect는 정렬된 리스트에서 특정 원소를 이진 탐색해주는 라이브러리입니다. 아래 그림을 통해 간단한 동작 예제를 보겠습니다.
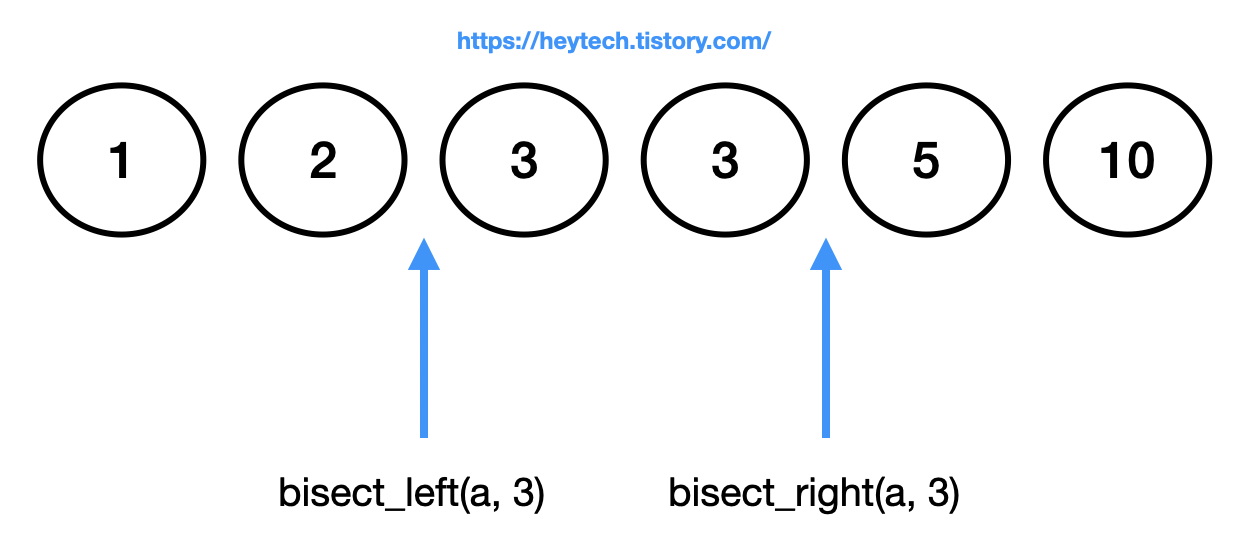
bisect_left(list, data) : 정렬된 리스트(list)에서, 정렬을 유지하며 data가 들어갈 가장 왼쪽 인덱스 리턴.
-> 위 예시에서 bisect_left(a,3)은 2를 리턴.
bisect_right(list, data) : 정렬된 리스트(list)에서, 정렬을 유지하며 data가 들어갈 가장 오른쪽 인덱스 리턴.
-> 위 예시에서 bisect_right(a,3)은 4를 리턴.
2) 사용할 변수 정의
N은 수열의 개수로 입력은 받지만 실제로 사용하지 않습니다. A는 입력받는 수열을 리스트로 만든 것입니다. dp는 가장 긴 증가하는 부분 수열을 저장할 리스트입니다.
2. 핵심 알고리즘
for num in A:
k = bisect_left(dp,num)
if len(dp) == k:
dp+=[num]
else:
dp[k]=numA를 for문으로 반복하며, 각 num에 대해 dp에 들어갈 알맞은 위치 k를 정합니다. (k는 인덱스)
k에 대해 경우에 따라 2가지 행동을 합니다.
1. k가 dp의 맨 오른쪽일 때 (if len(dp) == k)
이 때는, num이 dp의 최대값보다 큽니다. 그러므로, 맨 오른쪽에 추가해 줍니다. (dp+=[num] 이는 dp.append(num)과 동치)
2. 그 외에 num이 dp의 최대값보다 작은 경우 (else)
dp에 대해 알맞은 위치(k)에 num을 대치합니다. (dp[k] = num)
→ 대치 하지 않으면, num보다 크고, dp[k]보다 작은 수를 놓친다.
예를 들어, A=[10, 20, 15, 17, 20] 인 경우. num이 15일 때 dp는 [10, 20]으로 for문을 시작하며, k는 1입니다.
여기서, else로 빠져 dp[1]=15가 되지 않으면, 다음 for문에서 17을 놓치게 됩니다.
3. 생각해볼 점
이 문제의 가장 긴 증가하는 부분 수열은 영어로 LIS (Longest Increasing Subsequence)라고 불립니다.
여기서 dp의 길이는 LIS의 길이와 항상 같지만, dp와 LIS가 항상 일치하지는 않습니다. 그 이유는, 대치 과정 때문입니다. 반례를 하나 들자면, A가 [3, 4, 1] 일 때, for문을 돌다가 dp가 [3,4] 이고 num이 1일 때, k는 0이 될 것이고, 3은 1로 대치되어 마지막에 dp는 [1,4]가 될 것입니다. dp의 길이는 2로 LIS길이와 같지만, 그 내용은 [1,4]로 LIS [3,4]와 다릅니다. 아래 자세히 설명된 블로그가 있어 링크 첨부드립니다.
[최장 증가 수열] LIS(Longest Increasing Subsequence)
이번 글에서는 DP중에서 특별한 케이스인 LIS에 대해 얘기해보자 합니다. LIS(Longest increasing Subsequence)는 가장 긴 증가하는 부분 수열 정도로 해석 가능합니다. 쉬운 이해를 위해서 예를 들어보겠습
jason9319.tistory.com
읽어 주셔서 감사합니다.
오늘도 발전하는 당신을 응원합니다.
다음에 더 유익한 글로 찾아오겠습니다.
아래 주석과 함께 코드 설명된 깃허브링크를 첨부드립니다.
GitHub - netsus/BaekJoon: Algorithm Problem solving
Algorithm Problem solving. Contribute to netsus/BaekJoon development by creating an account on GitHub.
github.com
Reference)
1. 그림 1 : https://heytech.tistory.com/79
2. LIS 개념 : https://jason9319.tistory.com/113
'Programming > 알고리즘' 카테고리의 다른 글
| [백준] 1541 - 잃어버린 괄호 (Python, 숏코딩 2가지) (0) | 2022.04.24 |
|---|---|
| [백준] 9012 - 괄호 (Python, 숏코딩 포함) (0) | 2022.04.19 |
| [백준] 1003 - 피보나치 함수 (Python, 숏코딩 포함) (1) | 2022.04.18 |
| [백준] 1343 - 폴리오미노 (Python, 숏코딩 포함) (0) | 2022.04.13 |
| [백준] 2800 - 괄호제거 (Python, combinations) (0) | 2022.04.01 |